加速壽命測試中常用的失效分布模型主要包括以下幾類,它們適用于不同的失效機理和數據特征:
1. 指數分布(Exponential Distribution)
特點:
無記憶性(失效概率與時間無關)。
失效率恒定(λ),適用于早期隨機失效或電子元件的壽命分析。
應用場景:
電子元器件(如電阻、電容)的壽命測試。
簡單系統或組件的早期失效分析。
公式:
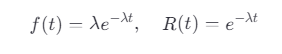
λ:失效率(尺度參數)。
2. 威布爾分布(Weibull Distribution)
特點:
β < 1:早期失效(如制造缺陷);
β = 1:隨機失效(類似指數分布);
β > 1:耗損失效(如疲勞、老化)。
靈活性強,可通過形狀參數(β)描述不同失效階段:
適用于復雜失效模式(如機械部件、電子器件)。
應用場景:
機械部件(軸承、齒輪)的疲勞失效;
電子產品的電遷移失效;
加速壽命測試中多階段失效分析。
公式:
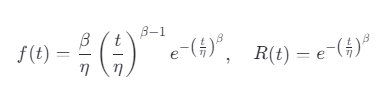
η:尺度參數(特征壽命);
β:形狀參數(失效階段判定)。
3. 正態分布(Normal Distribution)
特點:
對稱分布,適用于機械磨損類失效(如材料疲勞、尺寸變化)。
失效時間圍繞均值對稱分布。
應用場景:
機械部件的疲勞壽命測試(如彈簧、螺栓);
需要精確預測壽命均值和方差的場景。
公式:
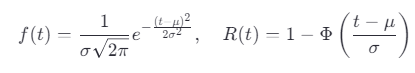
μ:均值(平均壽命);
σ:標準差(壽命離散程度)。
4. 對數正態分布(Lognormal Distribution)
特點:
對數變換后服從正態分布,適用于失效時間與對數變量相關的場景(如腐蝕、擴散過程)。
尾部較長,適合描述緩慢增長的失效過程。
應用場景:
化學腐蝕(如金屬氧化層退化);
材料疲勞(如裂紋擴展)。
公式:
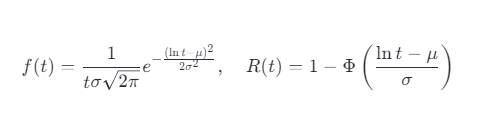
μ:對數均值;
σ:對數標準差。
5. Gumbel 分布(極值分布 I 型)
特點:
用于極值分析(如最大/最小失效時間)。
在加速失效時間模型(AFT)中常與指數分布或威布爾分布結合使用。
應用場景:
極端環境下的壽命預測(如高溫、高壓測試);
指數回歸模型和威布爾回歸模型的基礎。
公式:
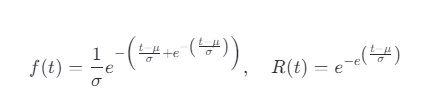
μ:位置參數;
σ:尺度參數。
6. Logistic 分布
特點:
尾部比正態分布更重,適合描述壽命分布具有長尾特征的場景。
在加速失效時間模型中用于構建對數logistic回歸模型。
應用場景:
生物醫學設備的壽命分析;
失效時間受多重因素影響的場景。
公式:
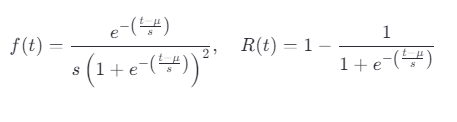
μ:位置參數;
s:尺度參數。
7. 廣義極值分布(Generalized Extreme Value Distribution, GEV)
特點:
統一了極值分布 I 型、II 型和 III 型,適用于不同類型的極值失效分析。
應用場景:
極端環境下的壽命預測(如航空航天設備)。
8. 二項分布(Binomial Distribution)
特點:
用于截尾試驗(如定數截尾樣本)的失效次數統計。
應用場景:
加速壽命測試中故障數的統計分析(如抽樣檢驗)。
公式:
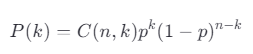
n:樣本總數;
p:單次試驗的失效概率。
選擇失效分布模型的關鍵因素
失效機理:
機械磨損(正態/對數正態) vs. 電子失效(威布爾/指數)。
數據特征:
是否存在早期失效(β < 1)或耗損失效(β > 1)。
測試目標:
需要預測平均壽命(正態/對數正態)還是可靠性置信區間(威布爾)。
實際案例
威布爾分布:
案例:汽車軸承的疲勞壽命測試。
結果:通過威布爾分布的形狀參數 β = 2.5 判斷為耗損失效,優化潤滑設計后 β 降低至 1.8。
指數分布:
案例:LED 驅動電源的高溫加速測試。
結果:失效率為 λ = 0.001/h,推算 MTBF = 1000 小時。
總結
在加速壽命測試中,威布爾分布和指數分布是最常用的失效分布模型,因其靈活性和廣泛的適用性。選擇時需結合失效機理、數據特性和測試目標,并通過統計檢驗(如卡方檢驗、Kolmogorov-Smirnov 檢驗)驗證模型的適用性。



